
Let's even look at your list of moments of inertia. Sure, technically, that is a very squat cylinder or a parallelepiped with a very thin depth, but if you use an MOI calculation for a 2-D object with a given mass per unit area, the answer between the 3-D and the 2-D calculations will be negligibly different - implying that the 2-D approximation is very, very good. Consider if I made a square and a circle out of very thin sheet metal. Genralz, in case you mean MOI of a cylinder or cubiod etc.īut I'm not just "making up a mass that has no meaning". Yes you can make up an mass that has no meaning, I don't care.
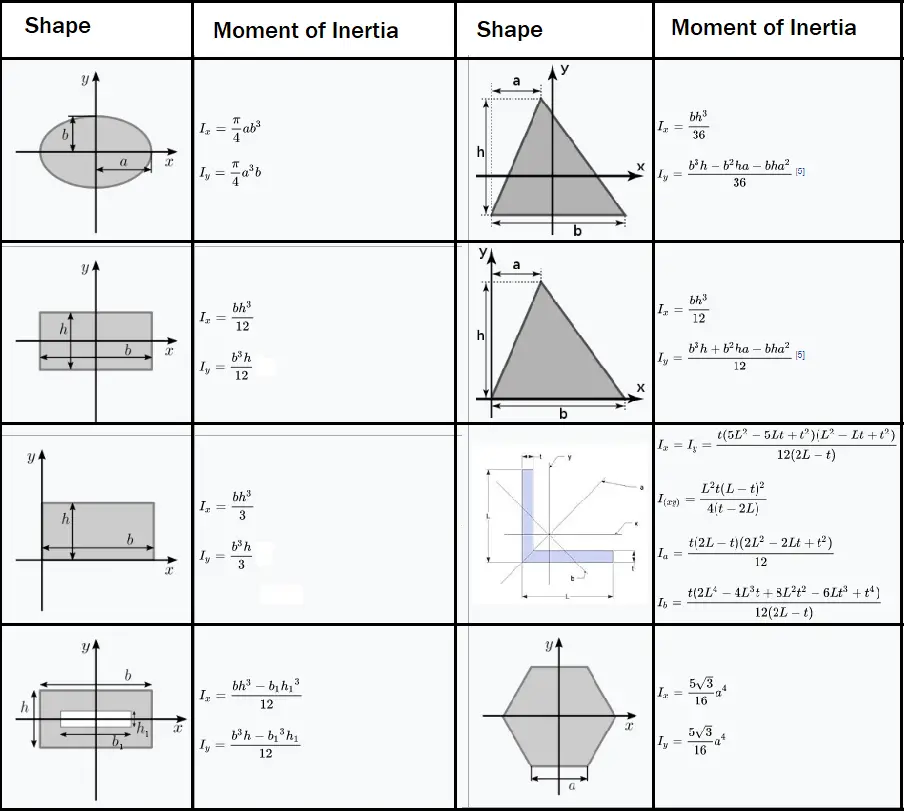
The simple fact is that the MOI formula requires a mass to have some meaning. To a very large extent, it doesn't really matter at all that no 2-D object has mass, or that there is no such thing as a perfect circle, mathematically such objects do exists and we can perform mathematics on them.įrom what I read genralz isn't interested in math for the math. It is a simplifying assumption made primarily to make the math easier and get a result that is going to be very close to the real world. Just like mathematically we can and do use point masses and point charges all the time, despite there being no such thing in the real world.
Mathematically we can assign an area density or mass per unit area and make it mathematically have mass. If you want to start down that road, why not just say that a circle or square can't have an MOI because there is no such thing as a perfect circle or perfect square? Kedas, while physically being merely a 2-D object a circle or square wouldn't have any mass in the real world, it doesn't prevent us from mathematically talking about a circle or square's MOI.
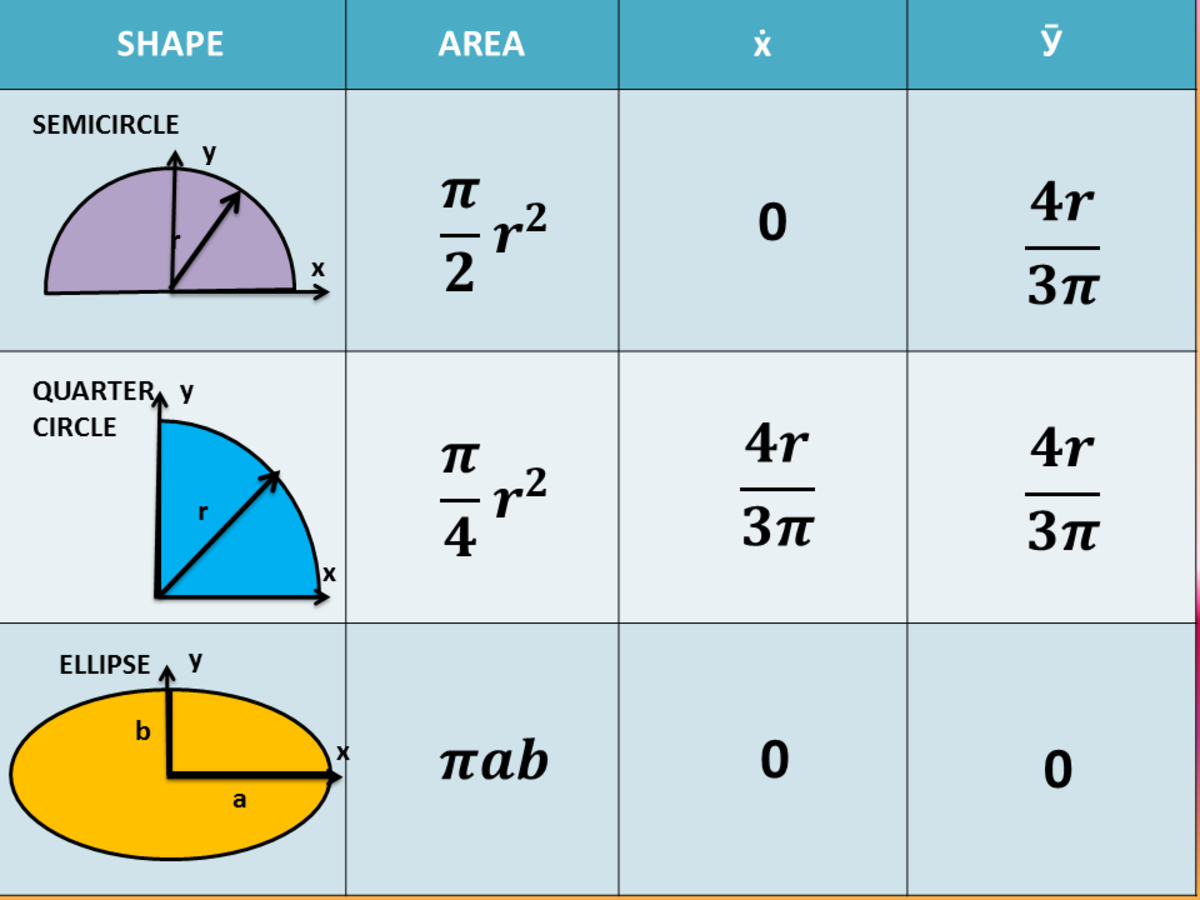
In this case, you can use vertical strips to find \(I_x\) or horizontal strips to find \(I_y\) as discussed by integrating the differential moment of inertia of the strip, as discussed in Subsection 10.2.3. When the entire strip is the same distance from the designated axis, integrating with a parallel strip is equivalent to performing the inside integration of (10.1.3).Īs we have seen, it can be difficult to solve the bounding functions properly in terms of \(x\) or \(y\) to use parallel strips. \newcommand\) then you can still use (10.1.3), but skip the double integration.


 0 kommentar(er)
0 kommentar(er)
